Du kan göra det eftersom din cykel är ansluten till marken.

Arbetet som utförs när du flyttar ett objekt är proportionellt mot avstånd och motståndskraft (som består av luftmotstånd och rullmotstånd för cyklar) . Luftmotståndet beror på lufthastighet (markhastighet + vindhastighet), men avståndet beror bara på markhastigheten. Att gå långsammare minskar den förbrukade energin, även när lufthastigheten förblir hög.

Som ett extremt exempel, överväga att bara stå på plats i vinden. Du gör inget arbete alls, men din lufthastighet är fortfarande hög. När du går mot vind kommer du snart att göra mer arbete. Och när du går medvind gör du negativt arbete!

För objekt som inte är anslutna till marken blir saker och ting annorlunda. En ballong i 40 MPH vind skulle driva 40 Mph nedvind i markkoordinater och skulle behöva använda samma kraft för att hålla sig på plats i markkoordinaterna som den skulle använda för att flytta 40 Mph i stillastående luft.

En numerisk exempel kan hjälpa. Vi känner till kraftekvationen för cyklar. För en cykel på plan mark, med jämn hastighet så att det inte finns någon acceleration eller retardation, vid lugna vindförhållanden, för typiska rullande och aerodynamiska dragkoefficienter för en platt barcykel (Crr ~ .005 och CdA ~ 0.4 m ^ 2) och en total massa på 85 kg är den effekt som krävs för att gå 30 mph (13,33 m / s):

.005 * 85 * 9,8 * 15,56 + 0,5 * 1,2 * 0,4 * 13,33 ^ 3 = 625 watt.

Vad skulle emellertid vara den kraft som krävs för att färdas vid 2,22 m / s till en vindvind på 30 mph? I så fall kommer flyghastigheten att vara 13,33 + 2,22 = 15,56 m / s men markhastigheten är bara 2,22 m / s.

.005 * 85 * 9,8 * 2,22 + 0,5 * 1,2 * 0,4 * (15,56 ^ 2) * 2.22 = 140 watt.

Du kan göra detta på grund av cykelns växel. När du kör med en lägre markhastighet, om du växlar till en lägre växel för att hålla din pedalvarvtal samma, ger samma kraft på pedalerna ett högre tryck på däcket. Även om du inte växlar är det lättare att producera högre kraft på pedalerna vid lägre varvtal.

Styrkan hos en cyklist mäts i allmänhet med den kraft de kan producera. Kraft = Force X-hastighet. I detta fall mäts hastigheten i förhållande till marken, eftersom cykeldrivanordningen fungerar genom att trycka på marken (via bakhjulet). Så om man åker 30 MPH i still luft på en plan mark och försummar rullmotståndet kräver 600 W kraft, krävs det att 5 MPH körs in i en 25 MPH motvind (samma dragkraft) (5/30) * 600 = 100 W.

Det beror delvis på hur vindhastigheten mäts. Standarden för vindhastighet är att mäta den 10 meter över marknivån. Närmare marken sparkar en effekt som kallas gränseffekten in och vindhastigheten är långsammare (i själva verket är vindhastigheten på marken faktiskt noll).

Enligt den här webbplatsen kan vindhastigheten på en plan gräsplan beräknas som V = Vref ((H / Href) ^ 0,142). För en Vref på 30 mph vid en Href på 10 m (ursäkta de blandade enheterna, de tappar ut eftersom ekvationen är dimensionell), skulle vindhastigheten 1 m från marken bara vara 21 mph.

Länken är dock föreslår också ett exponentvärde på 0,333 i utkanten av en stad eller 0,5 i en stad, vilket motsvarar vindhastigheter på 1 m eller 14 mph respektive 9,5 mph.

Så svaret på varför du kan trampa fortfarande framåt i en 30 mph motvind när du normalt är i jämvikt att trampa framåt vid 30 mph är att i fallet med motvinden kommer den faktiska vindhastigheten uppmätt vid din körposition bara att vara cirka 20 mph eller mindre.

Jag har en examen i kemiteknik och vi studerar detta inte bara i rörflöde utan i en fluidiserad katalytisk bädd och när du tappar katalysator ut ur skorstenen. I mina kemitekniska studier har vi aldrig behandlat partikelhastighet kontra vindhastighet annorlunda.

Enligt Galiliansk invarians ska du få samma vindmotstånd i vilken referensram som helst. Det är bara relativt. Tänk på det här vi snurrar och roterar runt solen.

Vindmotstånd är nätet. 30 mph i stillastående luft är exakt samma som 5 mph i 25 a mph huvudvind.

Gearing gör detta möjligt men det är inte den uttalade frågan. Frågan gäller enbart vindmotstånd:

30 mph (hastighet) + 0 mph (wind) = 5 mph (hastighet) + 25 mph (head wind)

Svaret är ja, de är desamma. Beviset är galilisk invarians.

Lägg 30,0 och 5,25 i denna miniräknare. Båda siffrorna ger samma relativa hastighet (30) och samma WATTS.

FLO Cykling - Hur hastighet påverkar Drag

Vid beräkning av drag , hastighet är inte bara den hastighet med vilken du reser på din cykel. Hastighet är kombinationen av hastigheten med vilken du reser på din cykel och vindens hastighet. Denna kombination av hastigheter är känd som relativ hastighet.
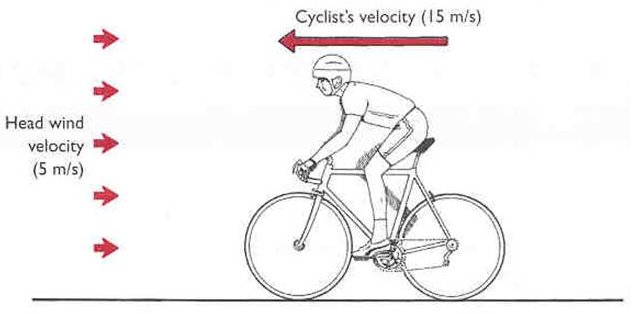I det här exemplet färdas cyklisten 15 km / h och vinden rör sig i motsatt riktning vid 5 km / h. Den relativa hastigheten är därför lika med ...
Rider Speed ​​- Head Wind
(15mph) - (-5mph) = 20mph

Dragstyrkor i formler

Effekten som krävs för att övervinna det totala motståndet är:
P = Ftotal v där v: hastighet i m / s
Formeln för luftmotstånd gäller strikt endast med vindstilla. Med vilken vind som helst måste vektorsumman av vind på grund av cykelns rörelse plus sann vind tas istället för v;

Drag (fysik)

avser krafter som verkar motsatt den relativa rörelsen för varje objekt som rör sig i förhållande till en omgivande vätska

v är hastigheten för objektet relativt till vätskan

Dragkoefficient

u, är objektets flödeshastighet relativt i förhållande till vätskan

proportionellt mot kvadraten på relativ flödeshastighet mellan objektet och vätskan

Dragkraft

v är kroppens hastighet i förhållande till vätskan stark>

Dragkraft och dragkoefficient

U är den relativa hastigheten för vätskan med avseende på partikel

Om du tappar en sten bör terminalhastigheten från gravitationen vara exakt densamma som vindhastigheten från en fläkt som krävs för att hålla den i luft.

Om den tredje V i effekt V³ är markhastighet och inte relativ hastighet hittar jag ingen referens som säger att. Låt oss anta att det är sant:
V _s1 är hastighet fortfarande
V _s2 är hastighet i vind
V _w är vindhastighet
V _s1 ^ 3 = (V _s2 + V _w ) * (V _s2 + V _w ) * V _s2
V _s1 ^ 3 = (V _s2 ^ 2 + 2 * V _s2 * V _w + V _w ^ 2) * V _s2
V _s1 ^ 3 = V _s2 ^ 3 + 2 * V _s2 ^ 2 * V _w + V _{w ^ 2 * V s2
om V s1 = 30 och V w = 25 då V s2 sub> = 16
Förmåga att rida 16 mph in i ett huvud 25 mph vind verkar inte vara rätt för mig men jag är bara inte så säker längre}

Den enda möjliga skillnaden är att vinden är något störd så det kommer att ha lite turbulens. Men med en liten hastighet är du i turbulent flöde (Reynolds nummer).

På grund av vindens stormiga och turbulenta natur kommer det att kännas snabbare än känslan av att åka i stillastående luft.

Antag att 30 netto mph är 600 watt

• Vid 30 km / h i 52 x 11 växlar
  kadens på 80
  jag levererar 600 watt

• Vid 5 km / tim i 26 x 33 växlar och kadens av 80
  Jag levererar 600 watt

Jag antar att din fråga är "Hur är det möjligt att jag fortfarande kan åka upprätt, även om motvinden är större än min maximala körhastighet?"

Svaret är:

• Vinden / vinden är inte alltid i konstant riktning och är verkligen inte ett konstant flöde (hastighet). Så den genomsnittliga motvindshastigheten är lägre än du antar. Detta gäller särskilt när du befinner dig i ett stadsområde, när vindriktningen ändras hela tiden.
• Även om det finns en konstant motvind på 30 km / h (din maximala körhastighet) går din hastighet inte plötsligt till noll. Din hastighet skulle gradvis minska, från hastigheten för dig och din cykel strax före bysten, tills den når noll. Analogin till den här situationen är när du rider med konstant 30 km / h och slutar trampa.

Så för att sammanfatta, har den genomsnittliga vindhastigheten inte tillräckligt med drag (kraft) för att nollställa hastigheten av dig och din cykel, som ständigt "fylls på" med din trampning.